Group Theory
Lie Group(리 군)에 대해 알아보기에 앞서 Group의 정의와 표현에 대해서 알아보고자 한다.
보통 matrix group에 우리가 관심을 가지는데 $SU_{(N)},O_{(N)},SP_{(N)},\cdots$ 들이 있는데 특히 $SU_{(2)}$와 $SU_{(3)}$에 대해서 아는것이 중요하다.
정의:
\[G=\{g_1,g_2,\cdots\} \\ {}^\exists{\cdot}:s.t. \\ (1) \ g_1\cdot g_2\in G \ (\cdot \ closed)\\ (2)\ (g_1\cdot g_2)\cdot g_3=g_1\cdot(g_2 \cdot g_3) \ (associativity) \\ (3) \ {}^\exists 1, g\cdot 1 = 1 \cdot g = g \\ (4) {}^\exists g^{-1},\ for\ all\ g\in G \ (x\cdot g = 1 \rightarrow x=g^{-1})\]위의 조건들을 만족하는 집합을 group이라고 부른다.
$O(N)$ Group
$O_{(N)}$ Group은 $AA^T=1$인 특성을 가지는데 $N$ dimensional vector space에서의 rotation group이다.
예를들어 $R\in3\times3$ 이면, $R$의 column들은 orthonormal basis 이며 각각의 column들은 orthonormal하다. 즉 $\hat{r_i}\cdot\hat{r_j}=\delta_{ij}$이며 $\Vert R\vec{X}\Vert=\Vert\vec{X}\Vert$이다.
$N$ dimension의 $\mathbb{R}$(orthonormal group)의 element가 몇개인가 = $\mathbb{R}$의 independent element가 몇개인가?
$\hat{r_i}\cdot\hat{r_j}=\delta_{ij}$가 constraint이므로 constraint의 갯수는 $N+\frac{1}{2}N(N-1)$이며 전체 원소의 갯수가 $N^2$이므로 $O_{(N)}$ group의 dimension은 $\frac{1}{2}N(N-1)$이 된다.
$U(N)$ Group
$U_{(N)}$ Group은 unitary group이라고 하는데 $UU^{\dagger}=U^{\dagger}U=1$을 만족하는 group이다.
$U$의 column들을 $\vec{a_i}$라고 하면 $(\vec{a_i},\vec{a_j})=\vec{a_i^*}\vec{a_j}=\delta_{ij}$가 constraint가 된다. 원래는 $N^2$개의 complex parameter가 존재하므로 $2N^2$개의 real parameter가 존재하게 된다. 그런데 constraint가 $i\neq j$인 경우 complex가 $\frac{1}{2}N(N-1)$개가 있으므로 parameter수는 2배인 $N(N-1)$ 이고 만약 $i=j$이면 real이 $N$개가 있으므로 총 $N^2$개의 constraint가 있게 된다. 그러므로 $\dim U_{(N)}=N^2$이다. $\det(U)=1$이라면 constraint가 추가되므로 이를 $SU_{(N)}$그룹이라 부르고 $\dim SU_{(N)}=N^2-1$이 된다. 이 추가된 constraint에 대해서 설명하자면
\[UU^\dagger=1 \\ \det U (\det U)^* =1 \\ \therefore \det U=e^{i\theta}\]원래 $U$의 determinant는 위와 같은데 $\theta=0$으로 정해지는 constraint가 생기면서 복소평면의 원 공간이 하나의 점으로 줄어들면서 차원이 하나 줄게된다.
Group Homomorphism
그룹 $G, G^\prime$가 있고 함수 $f:G→G^{\prime}$가 있을때
\[f(g_1)=g_1^\prime, f(g_2)=g_2^\prime \\ f(g_1)\cdot f(g_2)=f(g_1\cdot g_2)\]위의 조건을 만족하면 Group $G,G^\prime$가 homomorphic 하다고 하고 $f$를 homomorphism이라고 한다. 연산을 보존한다는 말로 두 그룹을 거의 같다고 봐도 된다는 얘기라고 한다. 만약 $f$가 1:1 대응이라면 isomorphism이라고 하고 두 그룹은 identical 하다고 한다.
Homomorphism of SU(2), O(3)
Pauli matrix라 불리는 특별한 matrix
\[\sigma_1 = \begin{pmatrix}0 & 1\\1 &0\end{pmatrix}, \sigma_2 = \begin{pmatrix}0 & -i\\i &0\end{pmatrix}, \sigma_3 = \begin{pmatrix}1 & 0\\0 &-1\end{pmatrix}\]들이 존재하고 다음과 같은 성질이 있다.
\[\sigma_1\sigma_2=i\sigma_3 \\ \sigma_2\sigma_3=i\sigma_1 \\ \sigma_3\sigma_1=i\sigma_2 \\ \sigma_1^2=\sigma_2^2=\sigma_3^2=1\]$M(\vec{\mathsf{x}})=\mathsf{x}_1\sigma_1+\mathsf{x}_2\sigma_2+\mathsf{x}_3\sigma_3=\vec{\mathsf{x}}\cdot\vec{\sigma}=\begin{pmatrix}\mathsf{x_3} & \mathsf{x_1}-i\mathsf{x_2}\\mathsf{x_1}+i\mathsf{x_2} & -\mathsf{x_3} \end{pmatrix}$ 라고 하고 $\vec{\mathsf{x}}\in\mathbb{R}^3$ 라고 하자. $\vec{\mathsf{x}^\prime}=R\vec{\mathsf{\vec{x}}}$ 라는 회전변환(SU(2))이 있고 이 값에 대응하는 $M(\vec{\mathsf{x}^\prime})$ 가 있다고 하면 $M(\vec{\mathsf{x}})$에 SU(2)를 곱해서 $M(\vec{\mathsf{x}^\prime})$를 만들 수 있을지 즉, 주어진 $R$에 대해서 적당한 $U$를 찾아 $M^\prime=M(\vec{\mathsf{x}^\prime})=UM(\vec{\mathsf{x}})U^\dagger$를 만족할 수 있을지를 알아보고자 한다.
In general 하게 푸는 것은 어렵기에 가장 간단한 rotation으로 z축으로 $\alpha$만큼 회전한 matrix $R$이 있다고 하고 $U$를 다음과 같이 정의해 본다.
\[R_z(\alpha)=\begin{pmatrix}\cos{\alpha} & -\sin{\alpha} & 0 \\ \sin\alpha & \cos\alpha &0 \\ 0&0&1\end{pmatrix} \\ U=\begin{pmatrix}e^{i\beta}&0\\0&e^{-i\beta}\end{pmatrix}\]$UMU^\dagger$를 계산해보면
\[U\begin{pmatrix}\mathsf{x_3} & \mathsf{x_1}-i\mathsf{x_2} \\ \mathsf{x_1}+i\mathsf{x_2} & \mathsf{x_3}\end{pmatrix}U^\dagger \\=\begin{pmatrix}e^{i\beta} & 0 \\0&e^{-i\beta}\end{pmatrix}\begin{pmatrix}\mathsf{x_3} & \mathsf{x_1}-i\mathsf{x_2} \\ \mathsf{x_1}+i\mathsf{x_2} & \mathsf{x_3}\end{pmatrix}\begin{pmatrix}e^{-i\beta} & 0 \\0&e^{i\beta}\end{pmatrix}\\=\begin{pmatrix}\mathsf{x_3} & e^{2i\beta}(\mathsf{x_1}-i\mathsf{x_2})\\e^{-2i\beta}(\mathsf{x_1}+i\mathsf{x_2}) & -\mathsf{x_3}\end{pmatrix}\]$RM$을 계산해보면
\[RM=\begin{pmatrix}\cos\alpha&-\sin\alpha&0\\\sin\alpha&\cos\alpha&0\\0&0&1\end{pmatrix}\begin{pmatrix}\mathsf{x}_1\\\mathsf{x}_2\\\mathsf{x}_3\end{pmatrix}=\begin{pmatrix}\cos\alpha\mathsf{x}_1-\sin\alpha\mathsf{x}_2\\\sin\alpha\mathsf{x}_1+\cos\alpha\mathsf{x}_2\\\mathsf{x}_3^\prime\end{pmatrix}\]이므로
\[\begin{pmatrix}\mathsf{x_3} & e^{2i\beta}(\mathsf{x_1}-i\mathsf{x_2})\\e^{-2i\beta}(\mathsf{x_1}+i\mathsf{x_2}) & -\mathsf{x_3}\end{pmatrix}=\begin{pmatrix}\mathsf{x_3}^\prime & \mathsf{x_1}^\prime-i\mathsf{x_2}^\prime \\ \mathsf{x_1}^\prime+i\mathsf{x_2}^\prime & \mathsf{x_3}^\prime\end{pmatrix},\\(\cos2\beta+i\sin2\beta)(\mathsf{x}_1-i\mathsf{x}_2)=(\cos2\beta\mathsf{x}_1+\sin2\beta\mathsf{x}_2)+i(\sin2\beta\mathsf{x}_1-\cos2\beta\mathsf{x}_2),\\\cos2\beta\mathsf{x}_1+\sin2\beta\mathsf{x}_2=\cos\alpha\mathsf{x}_1-\sin\alpha\mathsf{x}_2, \sin2\beta\mathsf{x}_1-\cos2\beta\mathsf{x}_2=\sin\alpha\mathsf{x}_1+\cos\alpha\mathsf{x}_2 \\ \beta=-\frac{\alpha}{2}\]이렇게 $U$를 구할 수 있고 다음과 같은 대응관계가 성립하고 둘 사이의 homomorphism을 찾은 것이다. $x,y$축에 대해서도 같은 식으로 구할 수 있다.
\[R_z(\alpha) \Longleftrightarrow U=\begin{pmatrix}e^{-i\frac{\alpha}{2}}&0\\0&e^{i\frac{\alpha}{2}}\end{pmatrix}\]지금까지 간단한 케이스로 이를 보였지만 $U=e^{i\alpha_i\sigma_i}$(여기서는 $i=3$ 에 대해서만 함)의 형태로 나타내고 $\alpha_i$가 주어지면 결국 이에 대응하는 $R$을 construction 할 수 있다. 여기서 $e^{i\alpha_i\sigma_i}$를 taylor expasion을 하면 $\sum\frac{(-1)^{n}\alpha_i^{2n}}{(2n)!}+i\sum\frac{(-1)^n\alpha_i^{2n}}{(2n+1)!}=\cos\alpha_i+i\sigma_i\sin\alpha_i$ 이다. $\sigma_i$는 hermitian matrix이므로 결국 임의의 unitary matrix는 hermitian matrix를 이용해 나타낼 수 있다($U=e^{i\alpha H}$ ). 정리하자면 unitary matrix를 hermitian matrix의 exponential 형태로 나타낼 수 있고 거기에서 $\alpha$가 주어지면 이에 대응하는 $R$을 찾을 수 있기에 SU(2)와 SO(3)는 homomorphic 하다고 볼 수 있다.
Lie Group, Lie Algebra
Lie Group은 노르웨이의 수학자 Sophus Lie가 고안한 이론으로 Lie는 갈로아가 발견한 다항식의 해를 찾는 공식이 존재하는 상황이 그 주어진 다항식의 해의 대칭성에 기인한다는 위대한 대수학의 발경에 감동을 먹고서 미분방정식에서도 대칭성의 이론을 찾아낼 수 있지 않을까하는 접근을 시도 하였다고 한다.
이러한 시도로부터 그는 기존의 유한 집합이 아니라 그룹의 원소가 무한대이고 오른쪽 혹은 왼쪽 이동에 대해서 대칭성을 가지고 연속적이며 미분가능한 smooth manifold가 되는 집합을 발견하게 되었고 우리는 이를 Lie Group이라 부른다.
그러면 이러한 Lie Group은 어떻게 얻는 것인가 하면 연속변환을 통해서 얻는다고 하는데 좌표변환을 생각해보면 기존의 좌표계에서 새로운 좌표계로의 선형변환을 우리는 주로 사용했는데 이러한 좌표변환이 한번만 일어나는것이 아니라 시간에 따라서 연속적으로 이루어진다고 하면 coordinate가 연속적으로 변하는 상황이 발생하고 이에 따라서 어떤 점 $P(x,y,z)$의 좌표 또한 연속적으로 변하게 된다. 그리고 이러한 변환에 의해 그려지는 $P$의 자취는 Lie Group을 이루게 된다. 예를 들어서 회전변환의 경우는 $[0,2\pi]$의 원모양의 smooth manifold가 된다. 이러한 관점은 공간에서 물체의 움직임도 이러한 연속변환의 관점에서 바라볼 수 있게 해주며 Lie Group에서의 미분이라는 해석적 접근을 가능하게 한다.
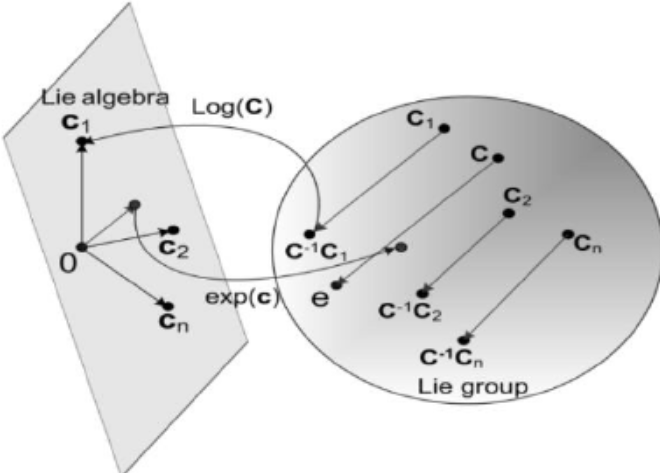
Lie Group중에서 특히 unitary 그룹을 예로 들면 $g=e^{i\epsilon h}$가 group element인데 여기서 $h$를 Lie algebra element라고 한다. 여기서 $\epsilon$이 매우 작다면 $e^{i\epsilon h}\approx 1+i\epsilon h$ 로 나타낼 수 있다. 그러면 $1+i\epsilon h$는 1(identity element) 근방의 어떤 값들이고 이 값들은 Lie Group의 identity element 에서의 tangent space 위에 있다고 할 수 있으며 이 tangent space의 원점은 identity element가 되며 이 tangent space위의 모든 점을 Lie Algebra라고 한다고 한다.
tangent space의 basis를 generator($S_i$)라고 하는데 $h=\sum\epsilon_iS_i$라고 나타낼 수 있고 이러한 generator의 linear combination을 이용해 Lie group을 만들고자 했다. 그리고 $[S_i,S_j]=\sum c_{ij}^k S_k$ 처럼 $S_i$와 $S_j$의 commutator를 $S_k$들의 linear combination으로 나타낼 수 있는데 그 이유는 $R_i=e^{\epsilon S_i}$라고 하면 $R_iR_jR^{-1}_iR_j^{-1}$는 $e^{\sum\delta_iS_i}$의 형태로 Lie Group의 또 하나의 element가 되는데 infinitesimal로 이 값을 계산하면 $1+\epsilon_i\epsilon_j[S_i,S_j]$이 되고 이게 결국 $1+\delta_iS_i$와 같아지므로 $[S_i,S_j]$를 다른 generator들의 linear combination으로 나타낼 수 있게 된다.
그래서 linear combination의 parameter에 의해서 Lie Algebra의 structure가 결정되고 이에 따라 Lie Group의 structure 또한 결정 된다. 따라서 Lie Group 상에서 어떤 문제를 풀기보다는 Lie Algebra 상에서 간단하게 풀어서 exponential을 통해서 Lie Group으로 변환할 수 있기에 Lie Algebra를 배우는 것이다.
\[SU(2)\ |\ su(2) \\ \begin{pmatrix}a & b \\ c & d\end{pmatrix} \ \ \ \ \ \ \sigma_1, \sigma_2, \sigma_3 \\ \dim SU(2)=3, \vec{M}(x)=\vec{x}\cdot\vec{\sigma}\]Lie Group의 곱셈 = Lie Algebra에서의 덧셈, su(2)의 generator(basis)는 pauli matrix이다.
\[g \leftarrow e^{M(x)} \\ \sigma_1\sigma_2=-\sigma_2\sigma_1=i\sigma_3 \\ [\sigma_1,\sigma_2] =\sigma_1\sigma_2-\sigma_2\sigma_1=2i\sigma_3 \\ [\frac{\sigma_i}{2},\frac{\sigma_j}{2}]=i\epsilon_{ijk}\frac{\sigma_k}{2}\]여기서 $\epsilon_{ijk}$는 structure constant라고 부른다. $H=\Sigma\alpha_iS_i$ 에서 $S_i=\frac{\sigma_i}{2}$이다.
지금까지 Lie Group에서 Lie Algebra로 변환하는 방법에 대해서만 배우고 Algebra가 vector space라는 것만 언급했는데 Algebra가 되기 위해서는 몇 가지 조건이 더 필요하다. 그래서 Algebra의 명확한 정의에 대해서 알아보고자 한다.
Algebra에서는 곱이 정의될 수 있는데 commutator로 정의된다. 두 element의 commutator를 취한 결과는 여전히 Lie Algebra의 element가 되는걸 앞에서 보였는데 이는 Lie Group의 closed-ness가 Lie Algebra의 곱을 commutator로 정의해 주는 것이다.
\[[S_i,S_j]=ic_{ij}^kS_k\]Jacobi Identity
\[[S_i,[S_j,S_k]]+[S_j,[S_k,S_i]]+[S_k,[S_i,S_j]]=0 \\ [S_i,[S_j,S_k]]=[[S_i,S_j],S_k]+[S_j,[S_i,S_k]] (Leibniz\ rule)\]→ group이 associative하기 위해서 algebra가 만족시켜야 하는 rule
SU(2)의 형태
\[su(2)\ \ \ \ \ \ \ \ \ \ \ \ M=i\vec{x}\cdot\vec{\sigma} \\ e^{M}=e^{\vec{x}\cdot\vec{\sigma}}=1+i\vec{x}\cdot\vec{\sigma} \\ g=y^0\cdot1+i\vec{y}\cdot\vec{\sigma}=\begin{pmatrix}iy_3+y_0 & iy_1+y_2 \\ iy_1-y_2 & y_0-iy_3\end{pmatrix}\]su(2)는 $\det{g}=1$이므로 $\det{g}=y^2_o+y^2_3+y^2_1+y^2_2=1$이 되어야한다. 이는 3차원 구 $S^3$의 형태로 생겼고 SU(2)와 SO(3) 또한 3차원 구처럼 생겼다고 봐고 된다.