이 논문들은 pointcloud registration의 조상격인 논문이다. 두 좌표계에 존재하는 point들의 registration 문제를 least square 문제로 바꿔서 iterative하게가 아닌 closed form으로 푸는 해법을 제시한 논문이라고 보면 된다.
Closed-form solution of absolute orientation using unit quaternions
paper: Closed-form solution of absolute orientation using unit quaternions
여기서는 solution을 unit quaternion의 형태로 rotation을 표현하며 4x4 matrix의 최대 eigenvalue의 eigenvector가 desired quaternion이 된다. 본 논문에서는 source와 target을 left와 right coordinate라고 표현하였다.
Method
앞으로 나오겠지만 scale factor와 translation은 rotation만 구하면 쉽게 구할 수 있으나 rotation을 구하는 것이 어렵다.
Selective Discarding Constraints
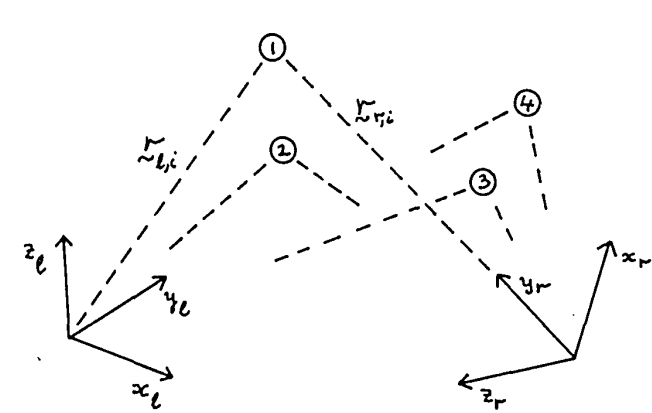
여기서는 3개의 point를(논문에서는 triad라 표현) 사용하여 각각의 coordinate를 기준으로 이 point들의 coordinate를 계산하였다. 이 triad point들의 left와 right 좌표계에서의 표현을 $r_{l,1},r_{l,2},r_{l,3},r_{r,1},r_{r,2},r_{r,3}$라 나타내었다.
\[x_l=r_{l,2}-r_{l,1}, y_l=(r_{l,3}-r_{l,1})-[(r_{l,3}-r_{l,1})\cdot\hat{x_l}]\hat{x_l}, \hat{z_l}=\hat{x_l}\times\hat{y_l} \\ x_r=r_{r,2}-r_{r,1}, y_r=(r_{r,3}-r_{r,1})-[(r_{r,3}-r_{r,1})\cdot\hat{x_r}]\hat{x_r}, \hat{z_r}=\hat{x_r}\times\hat{y_r}\]여기서 hat이 붙은 vector들은 unit vector이다. 그리고 이 column vector들을 합쳐서 matrix를 만드는데 다음과 같이 만든다.
\[M_l=|\hat{x_l}\hat{y_l}\hat{z_l}|, M_r=|\hat{x_r}\hat{y_r}\hat{z_r}|\]그리고 left coordinate상에서의 vector $r_l$을 이 triad point들의 coordinate로 변환하면 $M_l^Tr_l$이 되고 여기에 $M_r$를 곱하면 이 값들을 right coordinate에 mapping이 된다. 따라서
\[r_r=M_rM_l^Tr_l\]이 된다. 이를 통해 rotation은 다음과 같이 주어지는 것을 알 수 있다.
\[R=M_rM_l^T\]$M_r,M_l$은 만드는 과정에서 알 수 있듯이 orthonormal이므로 $R$ 또한 orthonormal이 된다. 이런식으로 rotation을 구하는 것은 쉽지만 data가 완벽하지 않을 경우 어떤식으로 3개의 point를 선택하느냐에 따라서 rotation matrix가 달라지므로 3개 이상의 point에 대해서는 확장을 하기가 어렵다. 그래서 이를 보완한 optimum rotation을 구하는 방법은 추후에 소개한다고 한다.
Finding the Translation
n개의 point가 존재한다고 할때 left와 right coordinate 에서의 point를 다음과 같이 나타낸다고 하자.
\[\{r_{l,i}\},\{r_{r,i}\}\]그리고 여기서 우리는 다음을 만족하는 transformation을 찾고자 한다.
\[r_r=sR(r_l)+r_0\]여기서 $s$는 scale factor $r_0$는 translational offset, $R(r_l)$은 $r_l$을 rotation한다는 의미이다. 모든 rotation에 대해서 rotation matrix는 orthonormal이므로 다음을 만족한다.
\[||R(r_l)||^2=||r_l||^2\]그리고 data가 완벽하지 않다면 최적의 transformation을 한다고 해도 residual error가 존재할 수밖에 없다. 이 residual error은 아래와 같이 나타낸다.
\[e_i=r_{r,i}-sR(r_{r,i})-r_0\]그리고 이 residual error의 sum을 minimize하는 것이 registration 문제를 푸는 것과 같다.
\[\sum_{i=1}^{n}||e_i||^2\]앞으로 우선은 translation에 대해서 그 다음은 scale 마지막으로 roataion에 대해서 total error가 달라지는 것을 살펴볼 것이다.
Centroids of the Sets of Measurements
각각의 coordinates 상의 point에 대해서 centroid $\bar{r_l},\bar{r_r}$를 계산하면 다음과 같다.
\[\bar{r_l}=\frac{1}{n}\sum_{i=1}^{n}r_{l,i}, \bar{r_r}=\frac{1}{n}\sum_{i=1}^{n}r_{r,i}\]그리고 이 centroid들을 중심으로 새로운 coordinate를 정의하고 여기서 point들을 나타내면 다음과 같아진다.
\[r^{\prime}_{l,i}=r_{l,i}-\bar{r_l}, r_{r,i}^{\prime}=r_{r,i}-\bar{r_r} \\ \sum_{i=1}^{n}r_{l,i}^{\prime}=0, \sum_{i=1}^{n}r_{r,i}^{\prime}=0\]그리고 residual error도 이 coordinate상으로 바꿔서 표현하면 다음과 같다.
\[e_i=r_{r,i}^{\prime}-sR(r_{l,i}^{\prime})-r_{0}^{\prime} \\ r_{0}^{\prime}=r_{o}-\bar{r_r}+sR(\bar{r_l}) \\ \sum_{i=1}^{n}||r_{r,i}^{\prime}-sR(r_{l,i}^{\prime})-r_{0}^{\prime}||^{2} \\ \sum_{i=1}^{n}||r_{r,i}^{\prime}-sR(r_{l,i}^{\prime})||^2-2r_{0}^{\prime}\cdot\sum_{i=1}^{n}[r_{r,i}^{\prime}-sR(r^{\prime}_{l,i})]+n||r_{0}^{\prime}||^2\]여기서 두번째 term은 centroid를 중심으로 coordinate를 옮겼으므로 0이 될 것이고 첫번째 term의 경우 translation과 상관 없는 term이며 마지막 term은 non-negative이므로 translation에 대해서 $r_0^{\prime}=0$일때 total error가 minimize되며
\[r_0=\bar{r_r}-sR(\bar{r_l})\]이 된다. 따라서 translation은 단순히 right centroid와 scaled, rotated left centroid 사이의 difference가 된다. 이 식은 scale과 rotation을 구한 이후에 translational offset을 구할때에 사용된다. 그리고 여기에서 $r_0^{\prime}=0$이므로 error term은 다음과 같이 나타낼 수 있다.
\[e_i=r_{r,i}^{\prime}-sR(r_{l,i}^{\prime}) \\ \sum_{i=1}^{n}||r_{r,i}^{\prime}-sR(r_{l,i}^{\prime})||^2\]Finding the Scale
\(||R(r_{l,i}^{\prime})||^2=||r_{l,i}^{\prime}||\) 이므로 total error를 전개하면
\[\sum_{i=1}^{n}||r_{r,i}^{\prime}||^2-2s\sum_{i=1}^{n}r_{r,i}^{\prime}\cdot R(r_{l,i}^{\prime})+s^2\sum_{i=1}^{n}||r_{l,i}^{\prime}||^2\]편의성을 위해 위의 식을 간단하게 나타내고 완전제곱식으로 바꾸면 다음과 같다.
\[S_r-2sD+s^2S_l \\ =(s\sqrt{S_l}-D/\sqrt{S_l})^2+(S_rS_l-D^2)/S_l\]이 식을 minimize하기 위해서는 $s=D/S_l$이 되어야 한다.
\[s=\frac{\sum\limits_{i=1}^{n}r_{r,i}^{\prime}\cdot R(r_{l,i}^{\prime})}{\sum\limits_{i=1}^{n}||r_{l,i}^{\prime}||}\]Symmetry in Scale
transformation은 inverse form의 형태로 대칭적으로 다음과 같이 나타낼 수 있다.
\[r_r=sR(r_l)+r_0 \\ r_l=\bar{s}\bar{R}(r_r)+\bar{r_0} \\ \bar{s}=1/s, \bar{r_0}=-\frac{1}{s}R^{-1}(r_0), \bar{R}=R^{-1}\]inverse transform에 대해서 위와 같은 식으로 $\bar{s}=\bar{D}/S_r$을 찾아서 구하게 되면 $\bar{s}\neq 1/s$ 가 된다. 그 이유는 위의 방식으로 하면 구해지는 scale이 각각의 coordinate에서의 measurement에 depend하기 때문이다.
위의 두 결과가 asymmetric해도 한쪽의 presision이 다른쪽에 비해서 매우 높다면 적절한 결과를 얻은 것이지만 두 measurement에서의 eror가 유사하다면 다음과 같은 symmetric error term을 사용하는 것이 더 합리적이다.
\[e_i=\frac{1}{\sqrt{s}}r_{r,i}^{\prime}-\sqrt{s}R(r_{l,i}^{\prime})\]위의 term을 사용하면 total error는 다음과 같아지며
\[\frac{1}{s}\sum_{i=1}^{n}||r_{r,i}^{\prime}||^2-s\sum_{i=1}^{n}r_{r,i}^{\prime}\cdot R(r_{l,i}^{\prime})+s\sum_{i=1}^{n}||r_{l,i}^{\prime}||^2 \\ =\frac{1}{s}S_r-2D+sS_l \\ =(\sqrt{s}S_l-\frac{1}{\sqrt{s}}S_r)^2+2(S_lS_r-D)\]$s=S_r/S_l$일때 최소가 된다.
\[s=(\sum_{i=1}^{n}||r_{r,i}^{\prime}||^2/\sum_{i=1}^{n}||r_{l,i}^{\prime}||^2)^{1/2}\]이 symmetrical result의 또 다른 장점은 rotation에 대해서 알 필요가 없이 scale을 구할 수 있다는 점이며 또한 scale의 결과가 rotation을 구하는데에 영향을 주지 않는다는 것이다. 그래서 결국 남은 error term을 minimize하기 위해서는 $D$를 maximize하는 rotation을 찾아야 한다. 즉 아래의 식을 maximize하는 rotation을 찾으면 된다.
\[\sum_{i=1}^{n}r_{r,i}^{\prime}\cdot R({r^{\prime}_{l,i})}\]Finding the Best Rotation
우선 본 논문에서는 rotation representation으로 quaternion을 사용했는데 그 이유는 unit quaternion 이라는 constratint가 rotation matrix가 orthonormal이라는 constraint보다 간단하기 때문이라고 한다. 그리고 unit quaternion의 axis와 angle notation geometric 관점에서 더 직관적이기 때문이다.
위의 식을 quaternion notation으로 바꾸면 다음과 같다.
\[\sum_{i=1}^{n}(\dot{q}\dot{r^{\prime}_{l,i}\dot{q}^*})\cdot\dot{r}^{\prime}_{r,i}\]이렇게 바꾸고 나면 위의 식을 maximize하는 unit quaternion $\dot{q}$를 찾는 문제가 된다. 그리고 이 식을 변형하면
\[\sum_{i=1}^{n}(\dot{q}\dot{r^{\prime}_{l,i}\dot{q}^*})\cdot\dot{r}^{\prime}_{r,i} \\ = \sum_{i=1}^{n}(\bar{Q}^{T}Q\dot{r}^{\prime}_{l,i})^T\dot{r}^{\prime}_{r,i} \\ =\sum_{i=1}^{n}(Q\dot{r}_{l,i}^{\prime})^T\bar{Q}\dot{r}^{\prime}_{r} \\ =\sum_{i=1}^{n}(\dot{q}\dot{r}^{\prime}_{l,i})\cdot(\dot{r}^{\prime}_{r,i}\dot{q}) \\ = \sum_{i=1}^{n}(\bar{\mathbb{R}}_{l,i}\dot{q})\cdot(\mathbb{R}_{r,i}\dot{q}) \\ = \sum_{i=1}^{n}\dot{q}^T\bar{\mathbb{R}}_{l,i}^T\mathbb{R}_{r,i}\dot{q} \\=\dot{q}^T(\sum_{i=1}^{n}\bar{\mathbb{R}}_{l,i}^T\mathbb{R}_{r,i})\dot{q} \\=\dot{q}^T(\sum_{i=1}^{n}N_i)\dot{q}\\=\dot{q}^TN\dot{q}\]이고 여기서
\[\bar{\mathbb{R}}_{l,i}=\begin{bmatrix}0 & -x_{l,i}^{\prime} & -y^{\prime}_{l,i} & -z^{\prime}_{l,i} \\ x^{\prime}_{l,i} & 0 & z^{\prime}_{l,i} & -y^{\prime}_{l,i} \\ y^{\prime}_{l,i} & -z^{\prime}_{l,i} & 0 & x^{\prime}_{l,i} \\ z^{\prime}_{l,i} & y^{\prime}_{l,i} & -x^{\prime}_{l,i} & 0 \end{bmatrix},\ \mathbb{R}_{r,i} = \begin{bmatrix} 0 & -x^{\prime}_{r,i} & -y ^{\prime}_{r,i} & -z^{\prime}_{r,i} \\ x^{\prime}_{r,i} & 0 & -z^{\prime}_{r,i} & y^{\prime}_{r,i} \\ y^{\prime}_{r,i} & z^{\prime}_{r,i} & 0 & -x^{\prime}_{r,i} \\ z^{\prime}_{r,i} & -y^{\prime}_{r,i} & x^{\prime}_{r,i} & 0 \end{bmatrix} \\ N_i=\bar{\mathbb{R}}_{l,i}^T\mathbb{R}_{r,i},\ N=\sum_{i=1}^{n}N_i\]이며 각각의 $N_i$들이 symmetric이므로 $N$ 또한 symmetric이다.
여기서 계산의 편리성을 위해서 다음과 같은 3$\times$3 matrix를 도입한다.
\[M=\sum_{i=1}^{n}r^{\prime}_{l,i}r^{\prime \ T}_{r,i} \\ M=\begin{bmatrix} S_{xx} & S_{xy}&S_{xz}\\ S_{yx}&S_{yy}&S_{yz}\\ S_{zx}&S_{zy}&S_{zz}\end{bmatrix},\ S_{xx}=\sum_{i=1}^{n}x^{\prime}_{l,i}x^{\prime}_{r,i}\]그리고 이 matrix $M$의 성분들을 이용해 $N$을 표현하면 다음과 같다.
\[N=\begin{bmatrix}(S_{xx}+S_{yy}+S_{zz})&S_{yz}-S_{zy}&S_{zx}-S_{xz}&S_{xy}-S_{yx}\\ S_{yz}-S_{zy} & (S_{xx}-S_{yy}-S_{zz})&S_{xy}+S_{yx}&S_{zx}+S_{xz}\\ S_{zx}-S_{xz} & S_{xy}+S_{yx}&(-S_{xx}+S_{yy}-S_{zz})&S_{yz}+S_{zy}\\ S_{xy}-S_{yx}&S_{zx}+S_{xz}&S_{yz}+S_{zy}&(-S_{xx}-S_{yy}+S_{zz})\end{bmatrix}\]이렇게 symmetric matrix $N$의 10개의 independent element를 $M$의 element를 이용해 나타낼 수 있으며 $Tr(N)=0$ 이다.
$N$은 4$\times$4 symmetric matrix이므로 4개의 real eigenvalue를 가지며 이를 크기 순으로 $\lambda_1,\lambda_2,\lambda_3,\lambda_4$라 하면 이와 관련된 unit eigenvector $\dot{e}_1,\dot{e}_2,\dot{e}_3,\dot{e}_4$에 대해서 다음을 만족한다.
\[N\dot{e}_i=\lambda_i\dot{e}_i,\ i=1,2,3,4\]임의의 quaternion $\dot{q}$는 이 eigenvector를 이용해 다음과 같은 linear combination으로 나타낼 수 있으며
\[\dot{q}=\alpha_1\dot{e}_1+\alpha_2\dot{e}_2+\alpha_3\dot{e}_3+\alpha_4\dot{e}_4\]이와 같은 식으로 $\dot{q}^TN\dot{q}$를 계산하면
\[N\dot{q}=\alpha_1\lambda_1\dot{e}_1+\alpha_2\lambda_2\dot{e}_2+\alpha_3\lambda_3\dot{e}_3+\alpha_4\lambda_4\dot{e}_4 \\ \dot{q}^TN\dot{q}=\dot{q}\cdot(N\dot{q})=\alpha_1^2\lambda_1+\alpha_2^2\lambda_2+\alpha_3^2\lambda_3+\alpha_4^2\lambda_4\]그리고 eigenvalue를 크기순으로 $\lambda_1 \ge \lambda_2 \ge \lambda_3\ge\lambda_4$ 이렇게 정했으며 $\dot{q}$가 unit quaternion 이므로 다음을 만족한다.
\[\dot{q}^TN\dot{q}\le\alpha_1^2\lambda_1+\alpha_2^2\lambda_1+\alpha_3^2\lambda_1+\alpha_4^2\lambda_1=\lambda_1\]따라서 $\dot{q}^TN\dot{q}$은 $N$의 가장 큰 eigenvalue $\lambda_1$보다 커질 수 없으며 이를 최대화 하기 위해서는 $\alpha_1=1,\ \alpha_2=\alpha_3=\alpha_4=0$이 되도록 해야 하므로 $\dot{q}=\dot{e}_1$이 residual error를 minimize하는 unit quaternion이 된다.
그리고 위에 구한 matrix들을 활용하여 이 eigenvector와 eigenvalue를 구하는 식은 다음과 같다.
\[\det(N-\lambda I)=0 \\ [N-\lambda_mI]\dot{e}_m=0\\\lambda^4+c_3\lambda^3+c_2\lambda^2+c_1\lambda+c_0=0\\c_3=0, c_2=-2Tr(M^TM),c_1=-8\det(M),c_0=\det(N)\]
Closed-form solution of absolute orientation using orthonormal matrices
paper: Closed-form solution of absolute orientation using orthonormal matrices
이 논문은 같은 저자가 1년뒤에 쓴 논문인데 앞에서 translation과 scale을 구하는 과정까지는 동일하며 rotation을 구하는 부분에서 quaternion representation 대신 orthonormal matrix representation을 사용해서 해결하였다. 따라서 앞부분은 생략하고 residual error를 minimize하기 위해서 maximize 해야하는 $D$를 다시 살펴보면 다음과 같다.
\[\sum_{i=1}^{n}r_{r,i}^{\prime}\cdot R({r^{\prime}_{l,i})}\]Dealing with Rodation
여기서 $a^TRb=Tr(R^Tab^T)$임을 이용하여(계산해보면 나온다) 위의 식을 정리하면
\[\sum_{i=1}^{n}r_{r,i}^{\prime}\cdot R({r^{\prime}_{l,i})}\\=\sum_{i=1}^{n}(r^{\prime}_{r,i})^TR(r_{l,i}^{\prime})\\=Tr\begin{bmatrix}R^T\sum\limits_{i=1}^{n}r^{\prime}_{r,i}(r^{\prime}_{l,i})^T\end{bmatrix}\\=Tr(R^TM)\]이고 여기서 $M$은 앞의 unit quaternion에서 구한 $M$과 같다.
\[M=\sum_{i=1}^{n}r^{\prime}_{r,i}(r^{\prime}_{l,i})^T \\ M=\begin{bmatrix} S_{xx} & S_{xy}&S_{xz}\\ S_{yx}&S_{yy}&S_{yz}\\ S_{zx}&S_{zy}&S_{zz}\end{bmatrix},\ S_{xx}=\sum_{i=1}^{n}x^{\prime}_{r,i}x^{\prime}_{l,i}\]여기서 $Tr(R^TM)$을 maximize하는 orthonormal matrix $R$을 찾으면 된다.
모든 square matrix는 orthonormal matrix $U$와 positive semidefinite matrix S로 decomposition할 수 있으며 matrix가 nonsingular라면 $U$가 uniquely determined 된다. 그래서 $M$이 nonsingular라면 다음과 같이 나타낼 수 있다.
\[M=US\\S=(M^TM)^{1/2},\ U=M(M^TM)^{-1/2},\ S^T=S,\ U^TU=I\]Symmetric matrix $S$
우선 $M^TM$을 eigenvalue와 eigenvector를 이용해 표현하면 다음과 같다.
\[M^TM=\lambda_1\hat{u}_1\hat{u_1}^T+\lambda_2\hat{u}_2\hat{u_2}^T+\lambda_3\hat{u}_3\hat{u_3}^T\]그리고 $M^TM$은 positive definite이므로 eigenvalue들이 positive이므로 eigenvalue의 square root들은 real value이며 다음과 같은 symmetric matrix $S$는 다음과 같이 나타낼 수 있다.
\[S=\sqrt{\lambda_{1}}\hat{u}_1\hat{u}_1^T+\sqrt{\lambda_{2}}\hat{u}_2\hat{u}_2^T+\sqrt{\lambda_{3}}\hat{u}_3\hat{u}_3^T\]$S^2=M^TM$임은 쉽게 알 수 있다. 그리고 $S$ 또한 positive definite 임은 다음과 같은 식으로 알 수 있다.
\[x^TSx=\sqrt{\lambda_1}(\hat{u}_1\cdot x)^2+\sqrt{\lambda_2}(\hat{u}_2\cdot x)^2+\sqrt{\lambda_3}(\hat{u}_3\cdot x)^2 > 0\]Orthonormal matrix U
모든 eigenvalue가 positive라면 다음과 같이 나타낼 수 있다.
\[S^{-1}=(M^TM)^{-1/2}=\frac{1}{\sqrt{\lambda_1}}\hat{u}_1\hat{u}_1^T + \frac{1}{\sqrt{\lambda_2}}\hat{u}_2\hat{u}_2^T + \frac{1}{\sqrt{\lambda_3}}\hat{u}_3\hat{u}_3^T\]그리고 다음과 같은 식으로 $U$을 구할 수 있다.
\[U=MS^{-1}=M(M^TM)^{-1/2}\]여기에 determinant를 적용하면
\[\det(U)=\det(MS^{-1})=\det(M)\det(S^{-1})\]$\det(S^{-1})>0$ 이므로 $\det(U)$와 $\det(M)$의 부호는 같으며 $\det(M)>0$ 이면 순수 rotation을 나타내고 $\det(M)<0$ 이면 reflection이 포함된 rotation을 나타낸다. 여기서는 data에 대해 rotation만 일어난다고 가정한다.
그리고 만약 $M$의 rank가 2라면 위의 방식으로 orthonormal matrix를 구할 수 없다. 그래서 대신 다음과 같은 식으로 구한다.
\[U=M\begin{pmatrix}\frac{1}{\lambda_1}\hat{u}_1\hat{u}_1^T+\frac{1}{\lambda_2}\hat{u}_2\hat{u}_2^T\end{pmatrix}\pm\hat{u}_3\hat{u}_3^T\]$\hat{u}_3$는 eigenvalute가 0인 eigenvector이다. 그리고 마지막 term의 부호는 $\det(U)$가 positive가 되도록 정한다.
다시 본론으로 돌아와 maximize하려는 값은 $Tr(R^TM)$이며 위의 decomposition을 적용하고 식을 정리하면 다음과 같다.
\[Tr(R^TM)=Tr(R^TUS)\\=\sqrt{\lambda_1}Tr(R^TU\hat{u}_1\hat{u}_1^T) + \sqrt{\lambda_2}Tr(R^TU\hat{u}_2\hat{u}_2^T) + \sqrt{\lambda_3}Tr(R^TU\hat{u}_3\hat{u}_3^T)\]그리고 trace는 commutative property를 만족하므로
\[Tr(R^TU\hat{u}_i\hat{u}_i^T)=Tr(\hat{u}_i^TR^TU\hat{u_i})=Tr(R\hat{u}_i\cdot U\hat{u}_i)=(R\hat{u}_i\cdot U\hat{u}_i)\]이며 $R,U$는 orthonormal이므로 $(R\hat{u}_i\cdot U\hat{u}_i)\le1$ 이며 equality가 성립하는 경우는 $R\hat{u}_i=U\hat{u}_i$ 일 때이다. 따라서 다음과 같은 식이 성립하며
\[Tr(R^TUS)\le\sqrt{\lambda_1}+\sqrt{\lambda_2}+\sqrt{\lambda_3}=Tr(S)\]$Tr(R^TUS)$의 maximum value는 $R^TU=I, R=U$가 되도록 $R$을 구함으로써 얻을 수 있다. 그래서 $M$이 nonsingular라면 우리가 구하고자 하는 orthonormal matrix $R$은
\[R=M(M^TM)^{-1/2}\]이다. $M$의 rank가 2라면 위에서 구한 방법대로 $R=U$로 구하면 된다.
Nearest Orthonormal Matrix
여기서는 $M$에 대해서 nearest orthonormal matrix $R$이 $U$와 같다는 것을 보인다. 이는 아래의 식을 minimize하는 $R$을 구한다는 것과 같다.
\[\sum_{i=1}^{3}\sum_{j=1}^{3}(m_{i,j}-r_{i,j})^2=Tr[(M-R)^T(M-R)] \\=Tr(M^TM)-2Tr(R^TM)+Tr(R^TR)\\ R^TR=I\]여기서 첫번째 term과 세번째 term은 $R$과 상관없는 term이므로 이 문제는 결국 $Tr(R^TM)$을 maximize하는 $R$을 찾는 문제와 같아지고 우리가 이제껏 풀었던 문제와 같은 문제이다.
이를 통해서 residual error를 minimize하는 orthonormal matrix는 원래의 matrix $M$에 가장 가까운 orthonormal matrix를 찾는 least-square 문제와 같다는 것을 알 수 있다.
Symmetry in the Transformation
left to right가 아닌 right to left transformation을 찾고 싶다면 다음 식을 maximize하는 rotation을 찾아야 한다.
\[\sum_{i=1}^{n}(r_{l,i}^{\prime})^T\bar{R}r_{r,i}^{\prime}\]앞에서 구한 rotation의 대칭성을 이용하면 바로 다음처럼 구할 수 있다.
\[\bar{R}=M^T(MM^T)^{-1/2}\]여기서 $\bar{R}^T=R$이 되어야하는데
\[\bar{R}^T=(MM^T)^{-1/2}M \\ R=M(M^TM)^{-1/2}\]위의 두 식이 달라보이지만
\[[M^{-1}(MM^T)^{-1/2}M]^2=M^{-1}(MM^T)^{-1}M=(M^TM)^{-1}\\ M^{-1}(MM^T)^{-1/2}M=(M^TM)^{-1/2} \\ (MM^T)^{-1/2}M=M(M^TM)^{-1/2}\]으로 같음을 알 수 있다.
위의 정보들을 바탕으로 실제로 rotation을 구하는 식은 다음과 같다.
\[M^TM=\begin{bmatrix}a & d& f \\ d& b& e \\ f& e& c\end{bmatrix}\\\det(M^TM-\lambda I)=0\\(M^TM-\lambda_i I)\hat{u}_i=0\\-\lambda^3+d_2\lambda^2+d_1\lambda+d_0=0\\d_2=Tr(M^TM)\\d_1=(e^2-bc)+(f^2-ac)+(d^2-ab)\\d_0=[\det(M)]^2\]